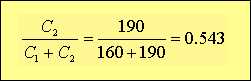よけいなお話７−１


さて、お客がものを買いに来るような問題では、客が買いに来る数量だけ在庫を持っていれば「何の過不足もない」ということになり、じつにハッピーな状態といえます。

しかし、一般的には不足が生じてもうけ損なったり、売れ残りが生じて損をしたりということになります。

アケミさんのケーキの場合、

原　価 ： １６０円／個
売り値 ： ３５０円／個

でしたから、

売れ残りの損失 ： Ｃ１＝１６０円／個
不足による損失 ： Ｃ２＝１９０円／個

と考えることができますね。そして

を計算して下さい。これがキーとなる数字です。なぜかは、ここでは話しません。


つぎに、毎日の需要 は一定の値ではなく、ある確率分布 にしたがう確率変数、つまり、気まぐれ変数というわけです。需要の実績データの相対頻度を計算し、これをその需要が起きる確率と読みかえます。需要が１０である確率は６０分の１で、０.０１６７と考えようというのです。

相対頻度は回数を計６０回で割った数値です。累積は順番に足していった数値です。最後は１になります。

表の累積値を上から順に見て、キーの数値より初めて大きくなるところを見つけてやります。

この問題の場合は１７個のところになります。これが損失最小にする最適な在庫量ということになります。

シミュレーション実験より手間がかかりません。

　

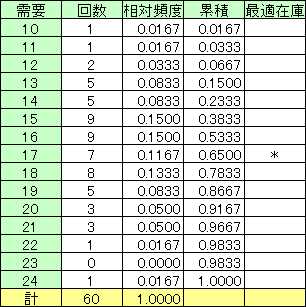
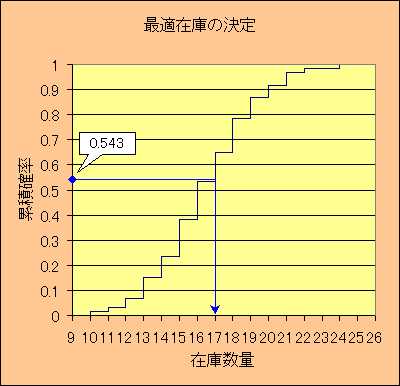
累積確率のグラフをかいたものです。離散的な分布ではこのような階段のグラフになります。縦軸にキーの値を定め、横軸と平行に線を引きぶつかった階段から真下におろしたところが最適な在庫量となります。　

最初、わたしたちは利益を最大にするにはどうすればよいかと問題を考えました。ここでは損失を最小にという具合に問題を設定してみました。ここでは、いずれからアプローチしても１７個作れという答えになり一致しました。しかし、一般には利益最大の答えと費用最小の答えは一致するとは限りません。

さらに「お客が買いに来たとき、目当ての商品がいつも売り切れている」という状態が起ると、客はつぎからよそに行ってしまうかもしれません。これは商売上好ましくありません。信用がなくなることにもつながりかねませんから、このような無形の損失も普通は考慮に入れるのです。アケミさんがこの損失をいくらと考えるかということです。もし、この損失を大胆にも２００円／個と見積もれば答えは変ってきます。

どうすればよいかは容易に分ることと思いますが、不足による損失にこの金額を含めてやればよいのです。

不足による損失 ： Ｃ２＝１９０＋２００＝３９０円／個

として、この問題を考えるだけでよいのです。そうすると、キーの数字は０．７１となります。その結果はグラフを眺めればただちに最適在庫＝１８個となります。

売れ残した場合、このケーキを作らずにその費用や時間を別のケーキをつくることに回すことができたら、あるいは他のものに投資をしてもうけることができたとしたら、C1はもっと高く見積もらなければならないでしょう。

このようにＣ１やＣ２のような問題のパラメータが変化したときに、最適解にどのような影響を与えるかを知っておくことは重要なことになりそうですね。このような分析を「感度分析」とよびます。その結果から、最も効果的な経営改善を行う指針が得られるわけです。

もし、売り切れになったとき、常連の客には「お電話で前の晩にでもご注文下さい」なんて気が利けばいいよね、アケミさん。

それから、「売り切れたケーキの場所に『売り切れ』なんて札が出ているところがありますが、あれはいけません。いかにもあるような体裁にしておかなくては。もし「月乃ひかり」ありますか、なんて尋ねられたときに潜在的に需要データを拾い集めておくことができます。これで、ここでやったような分析が可能となります。販売データと需要データは違うのです。よく、販売データを使って、それを外挿して需要予測だと思っている人が少なくありません。注意しましょう。

やれやれ、本当にめでたし、めでたし。