よけいなお話９

このような話は「信頼性理論」という分野にでてきます。信頼性の理論で扱う対象はシステムとよばれるものです。

人間に置き換えて考えてみると、こんな話になります。一つの仕事を２人の社員にやらせる案と４人の社員にやらせる案があるとします。そのグループの半数のものが間違った判断をしなければ、その仕事は成功するものとしましょう。

飛行機の例からわかるように、社員の信頼度が２/３以下であるならば、４人ではなく２人の方が失敗する確率が小さくなるのです。信頼度の高い社員ならば４人でやらせろといっているのです。

わたしの研究室では、卒論の学生のグループを組む時にこんなことを考えながら何人にしようか決めています。

人間に置き換えて考えると、なかなか含蓄のある話であることに気づくでしょう。

さて、システムを上手に設計する基礎的な話だけしておきましょう。イメージを浮かべていただきやすいように「スイッチ」を考えます。信頼度は ｐ だとしておきます。

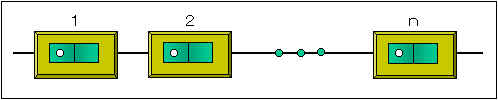
このスイッチをｎ個、直列に並べるとどんなことになるでしょう。

このように接続されたスイッチ・システムでは、どれか一つでもスイッチが壊れると電気はつきません。全体の信頼度Ｑ_直は、すべてのスイッチが完全である確率に等しくなりますから、

Ｑ_直＝ｐ^ｎ

となります。もし、ｐ＝０．９のスイッチを１０個、直列につなぐと０．９^１０＝０．３４８７となってしまいます。これでは用をなしません。

つぎに、スイッチを並列につなげてみます。このようにするとすべてのスイッチ壊れない限り電気はつきます。 並列回路の信頼度Ｑ並は、１−（すべてのスイッチ役立たずになる確率）ということになります。それは、 Ｑ並＝１−（１−ｐ）ｎ となります。ｐが１に近いと（１−ｐ）ｎは限りなくゼロに近づきます。ｐ＝０．９でｎ＝１０の場合ですと、Ｑ並＝0.9999999999となります。 おどろきですね。

ところで、スイッチとは電気をつけるだけの働きだけではなく、電気を切る働きもしているわけです。電気を切ろうとしているのに、切れないで点いてしまっても具合が悪いのです。

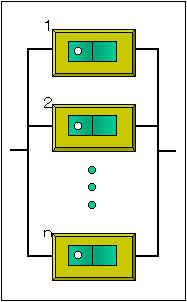
直列回路で切ろうとしたとき、すべてのスイッチが壊れない限り、電気は無事に消えてくれます。逆に並列回路の場合は、すべてのスイッチが働いてくれないと電気を切ることができません。

電気を点けようとしているのに点かないというエラーを「第一種の過誤」とよび、電気を消そうとしているのに点いてしまうエラーを「第二種の過誤」とよびます。

直列回路は第一種の過誤には弱いのですが、第二種の過誤には強く

並列回路は第二種の過誤には弱いのですが、第一種の過誤には強い

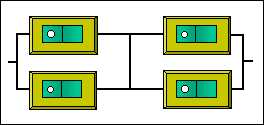
のです。したがって、エラーを起こさない強いシステムを設計するには、直列回路と並列回路を上手く組みあわせることを考えなくてはなりません。実際には単に直列・並列を組み合わせるだけでなく、ネットワークを設計することになってきます。一つのスイッチだけでもスイッチですが、余計にスイッチを用意すれば信頼性の高いスイッチ・システムを組み立てることが出るのです。余計なスイッチをたくさん用意することを「冗長性」を高めるといいます。Shannonは、どんなに低い信頼度の部品でも冗長性を高めることによって信頼性を高くすることが出来ることを示しました。

たとえば、スイッチが４個あるとき、つぎのように組み合わせて回路を作ると第一種の過誤も第二種の過誤も小さくすることが出来るのです。興味のある方は力試しに計算して確かめて下さい。

ちょっと、難しい話になりましたが、こういう原理を知っておかれると、いろいろな仕組みを考えるときに役に立つことになるかもしれませんね。会社のような組織はたくさんのスイッチ（従業員)からなり、それが階層構造になっているシステムのはずですよね。上のような組織図なんてあまりお目にかかりません。