|
|
つぎに、また右の図のようなカードをたくさん用意します。
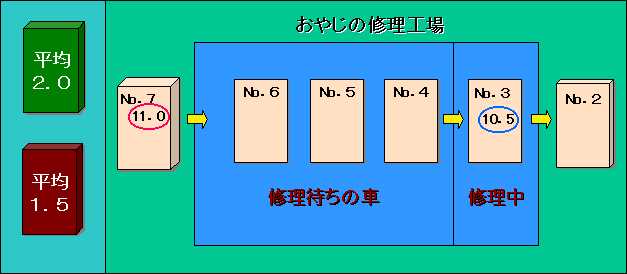
このカードは修理車の代用品です。 実験したい(台数+何枚か)分コピーして作っておきます。 これらのカードを下の図のように配置すると、この自動車修理工場の実験用の模型が出来上がります。この図は3台目の車が修理中の時点の修理工場の状態を表しています。 少し様子が分かってきたでしょう。 後は、この仕掛けが動くようにすればよいのです。このような仕掛けをシミュレーション・モデルと呼びます。 |
 |
こんな試し方、どう思います? |
|
名刺大のカードを、それぞれの気まぐれやさんのために100枚ずつ用意します。そして以下のように数字を書き入れてください。データのグラフの回数に比例するように枚数を決めています。
緑のカードと茶色のカードを別々に束にして、よくシャッフルして2山に積んでおいてください。これらの山から「ランダム」に1枚抜いては、また山に戻すという操作を繰り返します。そうすると、つぎつぎ出てくるカードの数値の列は、もとのパターンに従うことになりますね。 つまり、引き続く修理車の到着間隔やそれぞれの車の修理日数を元のパターンに従いながら、無作為に決めていくことができるわけです。 これは、これから行う実験のランダム・メカニズムとなります。 |
|
|
つぎに、また右の図のようなカードをたくさん用意します。
このカードは修理車の代用品です。 実験したい(台数+何枚か)分コピーして作っておきます。 これらのカードを下の図のように配置すると、この自動車修理工場の実験用の模型が出来上がります。この図は3台目の車が修理中の時点の修理工場の状態を表しています。 少し様子が分かってきたでしょう。 後は、この仕掛けが動くようにすればよいのです。このような仕掛けをシミュレーション・モデルと呼びます。 |
 |
| モデルの動かし方は以下の通りです。
① すべての修理車のカードを修理工場の左に積んでおきます。 ② 現時刻(本モデル内の時計)を時刻 T=0.0(日)にセットします。 ③ 到着間隔を決める緑のカードをランダムに1枚ぬき、
④ 修理中の車の修理終了日時と③で計算した到着日時とを比較します。 |
|
|
⑤ 予定した台数がまだ終了していない場合は、
⑥ 予定した台数が終了した場合は、ここでモデルを動かすのは停止します。
|